【Day 22】偏差與方差 Bias & Variance

15th鐵人賽機器學習偏差與方差

許皓翔

團隊最強資工大電神

2023-10-07 15:19:11

483 瀏覽

分享至

前言

昨天提到了模型欠缺擬和與過度擬和的問題，今天就要針對這兩個問題探討兩個評估模型效能的指標，分別是偏差 ( Bias ) 和方差 ( variance )，兩者對模型都算是誤差，所以希望越小越少，但通常在將低偏差的同時，方差就會提高，因此在偏差和方差之間大小的權衡 ( Trade-off ) 對模型的性能表現來說至關重要，注意到下圖的四個箭靶，藍點彼此之間的距離就為方差 ( Variance )，與紅色靶心的距離為偏差 ( Bias )：

欠缺擬和問題中的偏差與方差

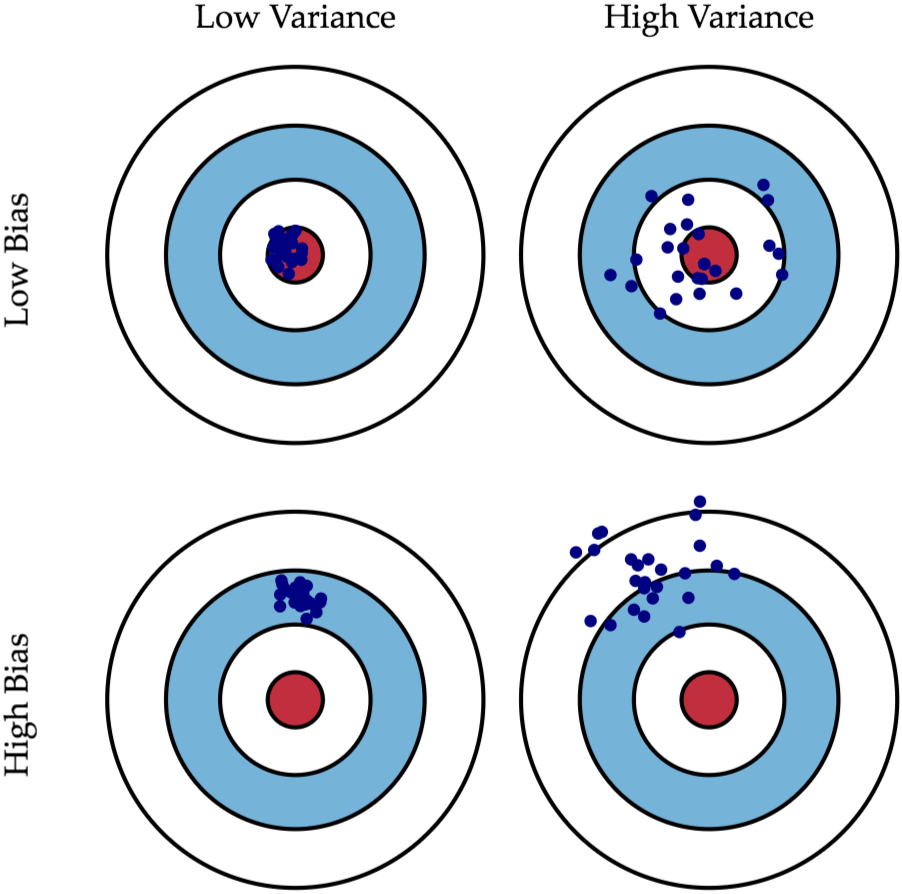
有欠缺擬和問題的模型其偏差大 ( High Bias )、方差小 ( Low Variance )，說明的就是上圖左下箭靶的情況：

欠缺擬和偏差

偏差 ( Bias )，代表著模型預測值與實際值之間的誤差偏離程度，就模型的欠缺擬和問題來說，因為在這個情況模型對訓練資料的擬和能力較弱，因此預測值和實際值之間的差距也較大，偏差也就跟著較大，通常這個時候的模型準確率也會較低，就像是你在考試前刷題目時，你可能領悟性較差、對範圍內容較不熟悉，又或者是較沒辦法掌握題目與答案之間的關係，你在做這些題目的時候都答錯一堆，成績不盡理想，換在機器學習中，就是模型無法準確地預測並擬和訓練資料，預測值和實際值之間存在著較大落差，也就是偏差 ( Bias )，在上圖左下箭靶中藍點就會離紅色靶心較遠，因為模型的擬和能力較差，就像你做再多的題目，你沒有能夠掌握正確答案的能力 ( 擬和能力 )，換做是用其它的資料集當作訓練資料，模型的擬和表現 ( 答題成績 ) 也是一樣欠佳，這就說明了模型的方差會小，上圖左下中的藍點彼此間距離也較小。

欠缺擬和方差

方差 ( Variance )，在統計學中可以用來表示資料的離散程度，欠缺擬和問題中指的就是模型在面對不同資料集時，因為模型本身輸出的預測值對於實際值的擬和表現欠佳，因此對於每個資料集模型的擬和表現欠佳的程度也會差不多，彼此間變異性就較小，方差也就較小，或許有點牽強，但這就像是你對考試範圍不熟時做好幾份題目成績都會不理想一樣，不會有哪幾份的成績會特別高 ( 差異性較小 )，方差就是表示了模型在不同的資料 ( 不同份題目 ) 表現的差異性。

過度擬和問題中的偏差與方差

有過度擬和問題的模型其偏差小 ( Low Bias )、方差大 ( High Variance )，說明的就是上圖右上箭靶的情況：

過度擬和偏差

剛剛提到欠缺擬和就像是你對考試範圍不熟，沒辦法答對許多題目，模型擬和能力就較低，但過度擬和是你為了要在答題上面取得較好的分數，當評估模型在訓練資料的表現時，因為這些資料你在訓練的時候就看過了，就像是你在考試前把所有考試會考的題目答案都記下來，在考試時因為這些題目你的看過了，所以成績必然較高，模型的預測值與實際值差距也較小 ( 偏差小 )，因此上圖右上箭靶中藍點就會較靠近紅色靶心，意味著模型在訓練資料上的表現會較好。

過度擬和方差

但如果你考前看的題目中有幾題的答案是錯的，你就會記下錯的答案，這會讓你在面對到題目從未見過的考試 ( 測試資料 ) 時，會讓你在作答時產生錯誤的判斷，這就是死記答案的後果，換做是模型也是如此，模型會因為會過度的擬和訓練資料，導致資料中若有存在的噪音，會很容易的被模型學習 ( 較敏感 ) 而影響其在測試資料上的表現，因為對於每個題目你都還沒完全的掌握住解題的訣竅，或者弄懂題目與答案之間的關係，只是單純把題目跟答案都死記硬背下來，換做模型也是一樣，模型始終沒有理解弄懂輸入特徵資料與輸出預測資料之間的關係而只是記下來，這樣會使得模型雖然可以較好擬和訓練資料，但是對於測試資料 ( 陌生資料 ) 的擬和能力卻很差，這就表示模型的方差較大，上圖右上箭靶中藍點彼此間距離也較大，代表模型的效能在在不同的輸入資料的表現差異較大。

偏差與方差之間的權衡 ( Bias-Variance Trade Off )

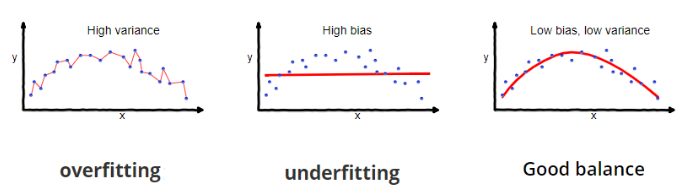
因為大的偏差就會導致方差較小，小的偏差就會導致較大方差，因此我們希望能在這兩者之間取得平衡，找到最理想的組合，避免極端的情況出現，也就是過度擬和 ( 下圖最左 ) 和欠缺擬和 ( 下圖中間 )，我們要讓模型不要只是把訓練資料的結果死記下來，要掌握住資料中的模式或趨勢，推理出能夠讓預測值準確的竅門，這樣就可以避免在面對不同的陌生資料時用死板框架去預測，而是要靈活地去擬和各種不同資料，我們在訓練模型目的就是為了找出一個能夠在偏差與方差之間取得平衡 ( Good balance ) 的最佳函數，這個函數不管是在訓練資料還是測試資料中都能夠很好的擬和，能夠有較低的偏差和較低的方差，就是下圖最右邊的情況。

模型複雜度的影響

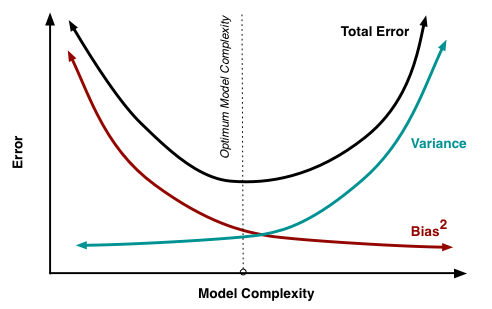
模型不同的複雜度會分別對應不同的偏差與方差，最後得到總體的誤差 ( Total Error )，反映模型的效能表現，上圖的中間那條虛線，代表了模型在最小誤差下的複雜度，在這複雜度下的模型其偏差與方差為最理想，模型的表現最佳，從虛線的左側移動到右側，說明了模型從欠缺擬和到過度擬和的過程，過低的模型複雜度對導致欠缺擬和，過高的複雜度會導致過度擬和，因此找出最佳的模型複雜度至關重要，讓模型效能可以最佳並且損失較小。